Poderemos dizer que existem equações bonitas na matemática? Os cientistas dizem que sim
Foram reveladas as equações mais bonitas, estimulantes e convincentes, segundo os matemáticos. Fique aqui a conhecer algumas delas!
Os matemáticos olham para as equações como arte. Assim como muitos se comovem com uma pintura ou uma peça de música, para aqueles que apreciam e compreendem a matemática, as expressões de números, variáveis, operações e relações entre quantidades podem ser igualmente atraentes.
Tal como acontece com a beleza artística, "a beleza matemática está nos olhos de quem a vê", e um matemático pode valorizar equações simples e sucintas, enquanto outro pode preferir o oposto.
Desta forma, quer as equações antigas como as contemporâneas são admiradas pela sua inteligência, poder e possibilidade.
Equação Diferencial de Loewner
A equação diferencial de Loewner, foi introduzida por Charles Loewner em 1923, e descreve a evolução temporal de uma família de funções conformes (que preservam o ângulo) definidas em subconjuntos do plano complexo.
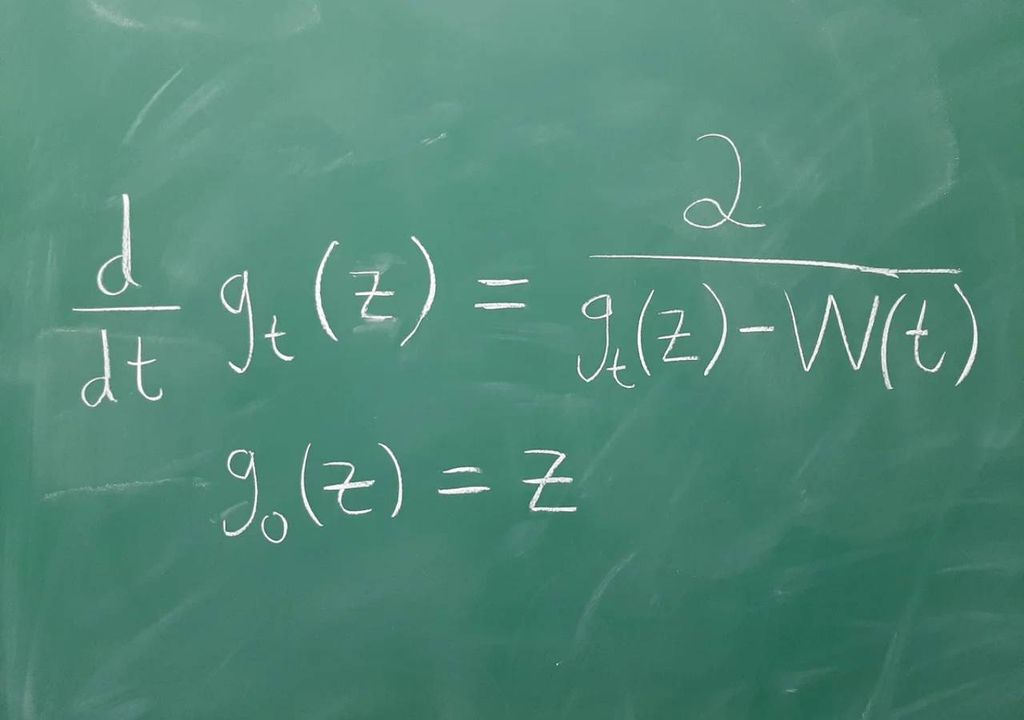
Quase 80 anos mais tarde, em 1999, Oded Schramm descobriu que a solução da equação de Loewner tem simetrias especiais quando a função motriz é considerada um movimento browniano, uma função aleatória que é um objeto central de estudo na teoria das probabilidades.
Com base na descoberta de Schramm, provou-se que a solução da equação de Loewner para esta escolha de função motriz, denominada evolução de Schramm-Loewner, descreve o comportamento em grande escala de vários modelos críticos na mecânica estatística bidimensional.
Assim, esta equação revolucionou o estudo matemático da mecânica estatística e conduziu a algumas das descobertas mais interessantes da matemática nas últimas duas décadas, segundo Ewain Gwynne da Universidade de Chicago.
Equação de Gauss-Bonnet
A fórmula de Gauss-Bonnet é uma bela equação em geometria diferencial que afirma a igualdade do integral da curvatura de Gauss sobre uma superfície e uma constante multiplicada pela caraterística de Euler da superfície.
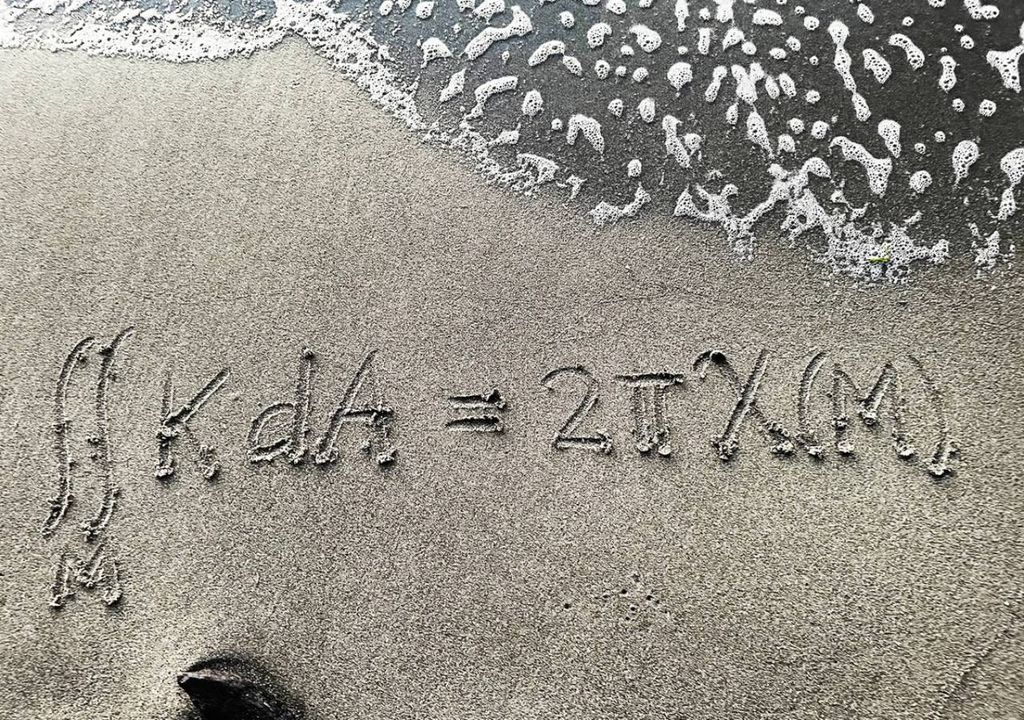
A equação é notável porque relaciona duas quantidades muito diferentes: a curvatura da superfície, por um lado, e a topologia da superfície, por outro.
A característica de Euler é um invariante topológico global da superfície que descreve a estrutura topológica da superfície, independentemente da forma como é curvada.
De acordo com Ailana Fraser da Universidade de British Columbia, alguns dos aspetos mais bonitos desta equação são a simplicidade da sua expressão.
Uma soma infinita
Esta função importante e aparentemente básica, que tem a ver com a adição e a contagem, é bela e talvez inesperadamente complexa.
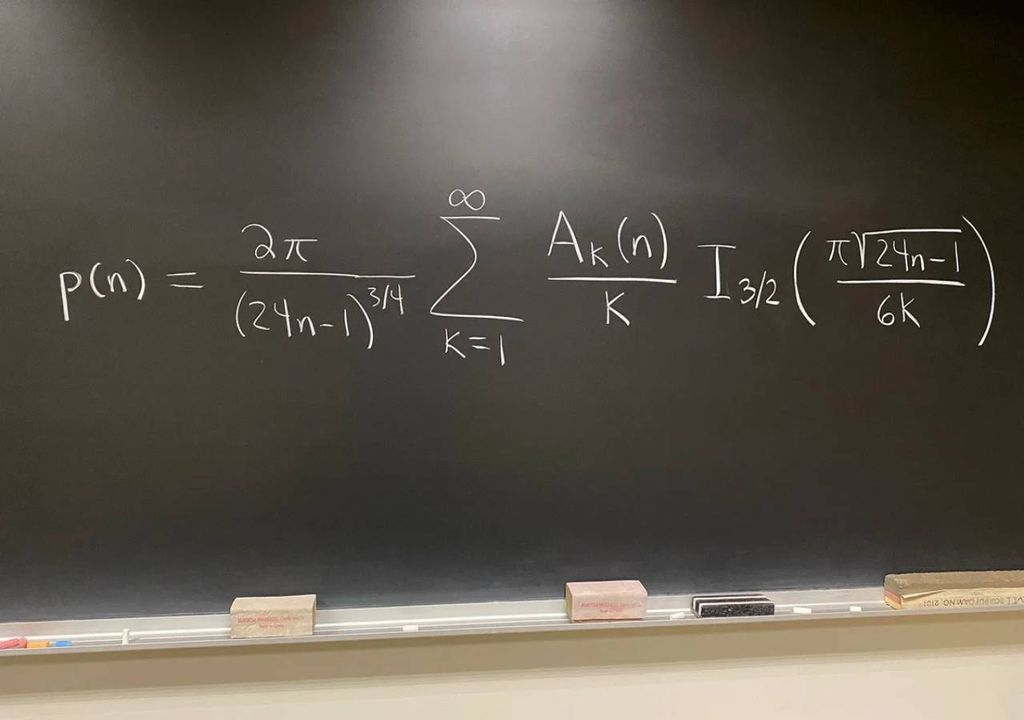
O lado direito desta equação é uma fórmula exata para graças ao trabalho, em 1937 de Hans Rademacher.
Alguns podem considerar o (grande) lado direito, uma soma infinita que envolve somas de números complexos (imaginários) (Ak(n)), potências fraccionárias (3/4 e a raiz quadrada), o número transcendental pi, entre outros, como o oposto de belo ou como intimidante - especialmente porque substitui o lado esquerdo (visualmente pequeno) que até uma criança consegue compreender.
Amanda Folsom do Amherst College, afirma que é bonito o facto de a soma infinita que aqui aparece convergir, o que significa que soma algo finito, um número real que conta algo de importante, e que não continua a acumular-se.








