O que uma equação com 190 anos sobre tempestades nos pode dizer

Decorria o ano de 1835 quando o engenheiro e físico francês Émile Clapeyron descobriu porque é que a pressão reduzida em altitude afeta o ponto de ebulição da água, ao ponto desta ferver mais rapidamente com uma temperatura inferior.

O seu trabalho acabou por estabelecer a relação entre a pressão de uma substância e a temperatura, quando duas fases dessa substância se encontram em equilíbrio. A relação é agora conhecida como a equação de Clausius-Clapeyron.

O impacto desta equação atualmente

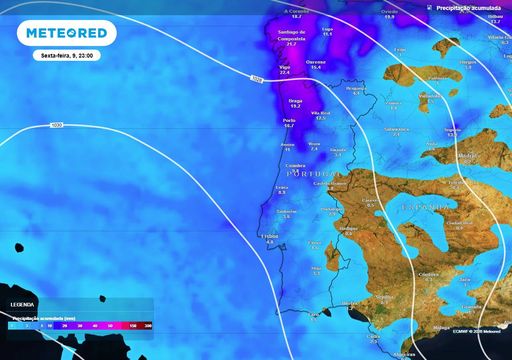
Quase 200 anos depois, esta relação está a ajudar os climatologistas a compreender os efeitos das alterações climáticas. A equação mostra como o ar mais quente pode conter mais humidade, o que é crucial para prever o aumento da força das tempestades e a maior intensidade da precipitação.

"Um ponto chave sobre esta equação é que ela tem um exponencial lá dentro", diz Peter Stott, um climatologista do Gabinete Britânico de Meteorologia. "Uma curva exponencial, claro, sobe mais acentuadamente quanto mais se sobe. Então, à medida que a temperatura aumenta, o nível de precipitação acompanha este aumento".

Portanto, a equação aponta para um futuro mais húmido, mas como os investigadores começam a perceber, isto é apenas o início. As tempestades futuras podem produzir ainda mais chuva do que a equação prevê.

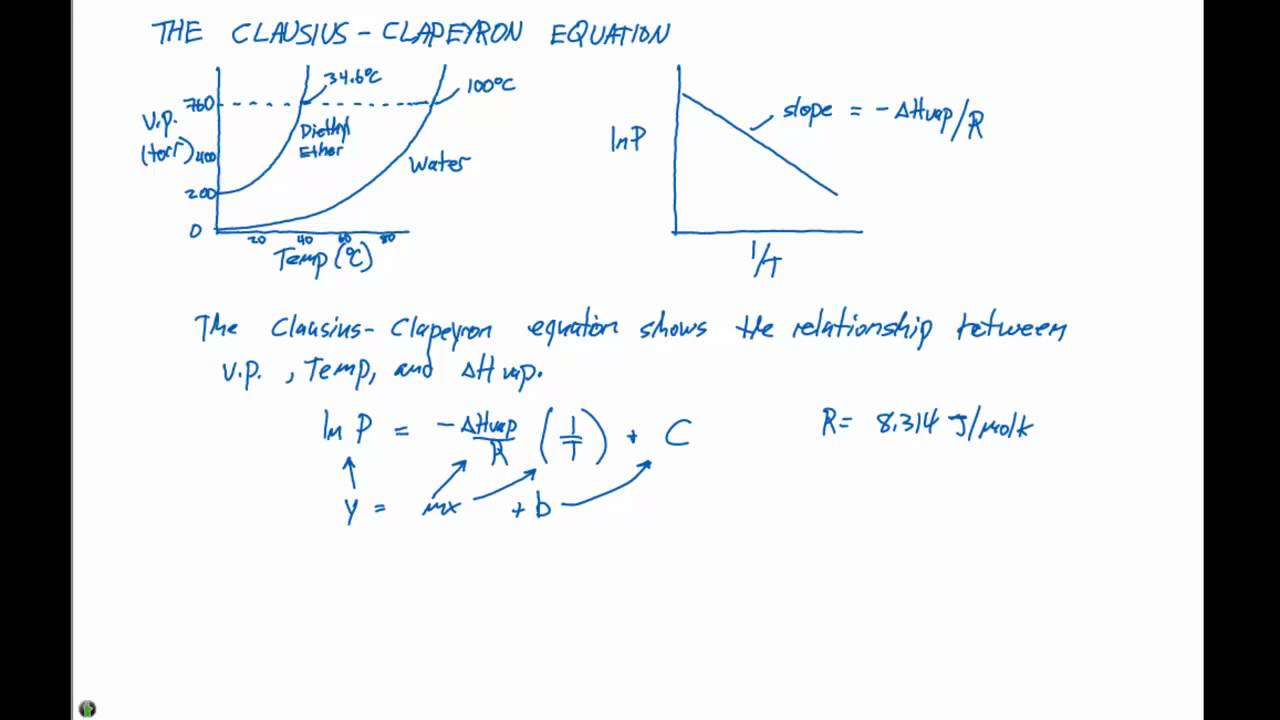
A equação de Clausius-Clapeyron

Era a idade da máquina a vapor. Um grupo de cientistas composto por Sadi Carnot, James Joule, William Rankine e William Thomson, assim como Émile Clapeyron e Rudolf Clausius, trabalharam em teoria e aplicações práticas para tentar melhorar a eficiência desta tecnologia crucial.

Clapeyron foi um dos primeiros a considerar a teoria de como os estados gasoso e líquido da água se comportam enquanto este fluido é aquecido dentro de uma máquina a vapor. Em 1834, ele tinha teorizado de que forma a pressão do vapor - que é a pressão exercida pelo vapor quando em equilíbrio com o líquido - poderia mudar com a temperatura.

Em 1850, Clausius refinou a relação para incluir o calor latente, a energia necessária para vaporizar uma determinada quantidade de líquido, para dar a forma da equação que usamos hoje.

Esta equação pode explicar observações diárias, como, por exemplo, uma panela de pressão poder acelerar as refeições ao fazer a água ferver a 120 °C. Os cientistas de várias disciplinas utilizam-na para calcular tudo, desde a composição provável de atmosferas e oceanos noutros planetas, até ao potencial energético.

Contudo, uma das suas utilizações mais importantes é na meteorologia, particularmente em simulações de como a atmosfera e o clima irão responder às alterações climáticas.

Os meteorologistas utilizam a equação de Clausius-Clapeyron para compreender em que momento o vapor de água se condensará para o estado líquido. Isto acontece devido à pressão de vapor de saturação, a pressão máxima que pode ser exercida pelo vapor de água antes de se condensar. A equação mostra que esta pressão aumenta exponencialmente com a temperatura.

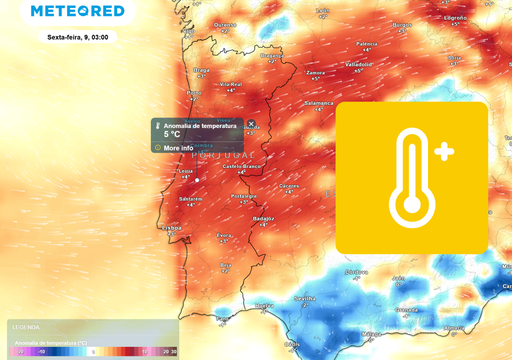
A equação mostra que para cada grau Celsius extra de aquecimento, o ar pode conter mais 7% de água. Pelo que com 2 °C de aquecimento global, o mundo poderia esperar mais 14% de humidade no ar, e com 3 °C de aquecimento, esse valor seria de 21%, e assim sucessivamente.

As tempestades atualmente

Grande parte das fortes chuvas e inundações observadas na Califórnia, nos últimos meses e anos, tiveram origem em eventos que começaram sobre o oceano, e assim transportaram a quantidade total de vapor de água extra, prevista pela equação de Clausius-Clapeyron.

Estas tempestades são impulsionadas pela deslocação de longas e estreitas colunas de vapor de água chamadas de rios atmosféricos, que muitas vezes têm origem nos trópicos.

"O aumento global da temperatura está mais próximo de 1,2 graus, pelo que há, provavelmente, 8% mais humidade nos rios atmosféricos agora do que teria havido sem as alterações climáticas", diz Stott.

Porém, às vezes o aumento da precipitação é menor do que o previsto pela equação, devido a um aspeto físico pouco compreendido pela ciência das nuvens chamado eficiência da precipitação.

Em suma, nem todo o vapor de água condensado do ar chega de facto ao solo como chuva ou neve, pois parte dele reevapora-se.